Chapter 5 Logistic Regression
5.0.1 Simple Example
Generating data
Estimating model coefficients
##
## Call:
## glm(formula = Y ~ X, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4713 -0.6868 -0.3107 0.6862 2.4725
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.0096470 0.0198147 -151.9 <2e-16 ***
## X 0.0601529 0.0003612 166.5 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 138629 on 99999 degrees of freedom
## Residual deviance: 93059 on 99998 degrees of freedom
## AIC: 93063
##
## Number of Fisher Scoring iterations: 4MLE for beta
## (Intercept) X
## -3.00964698 0.06015287New Data
new.data=data.frame(X=1:100)
# Estimating g for New Data
ghat=cbind(1,1:100)%*%betahat
plot(1:100,ghat,type="l",col="red")
ghat=predict(model,newdata=new.data)
plot(1:100,ghat,type="l",col="red")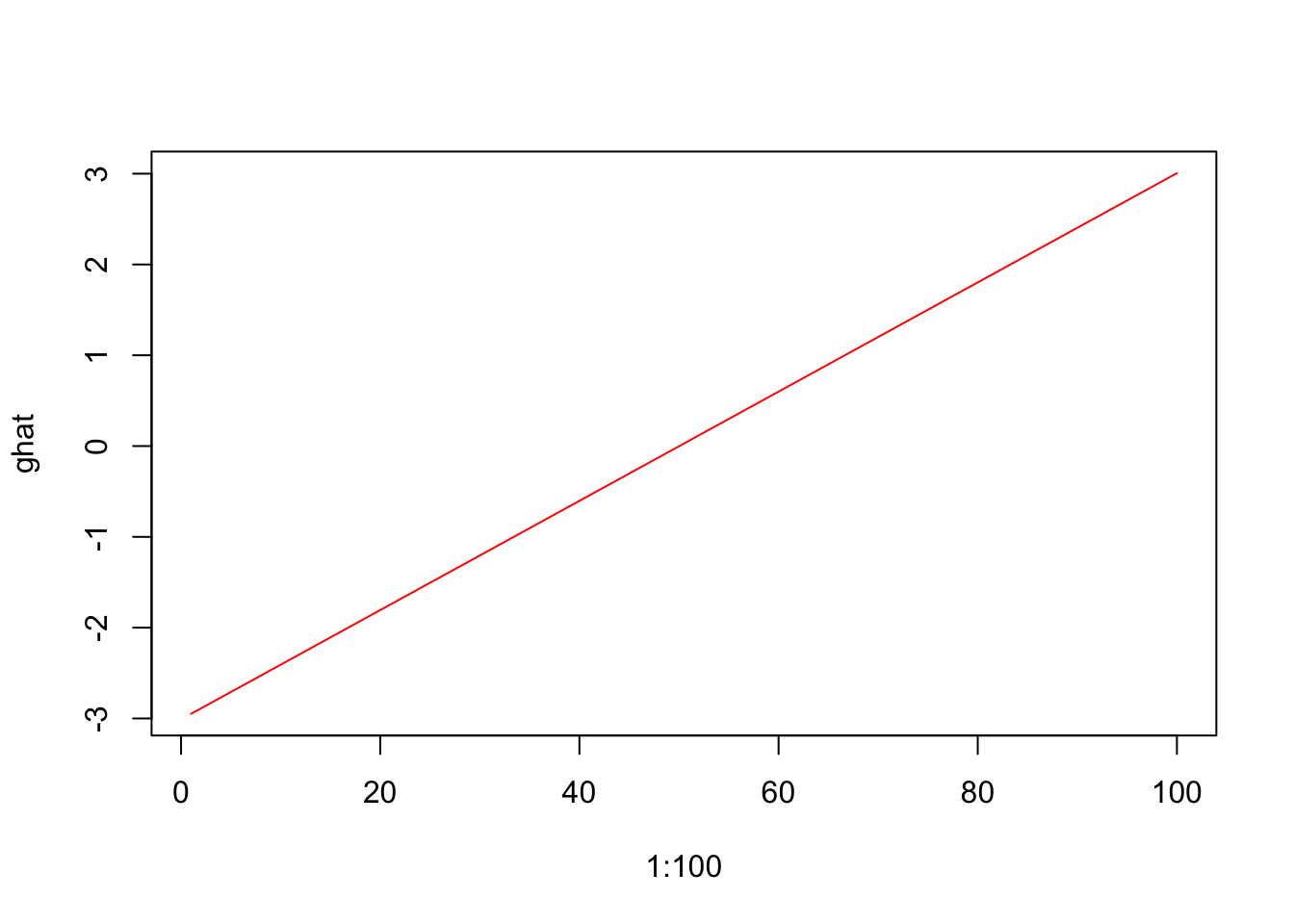
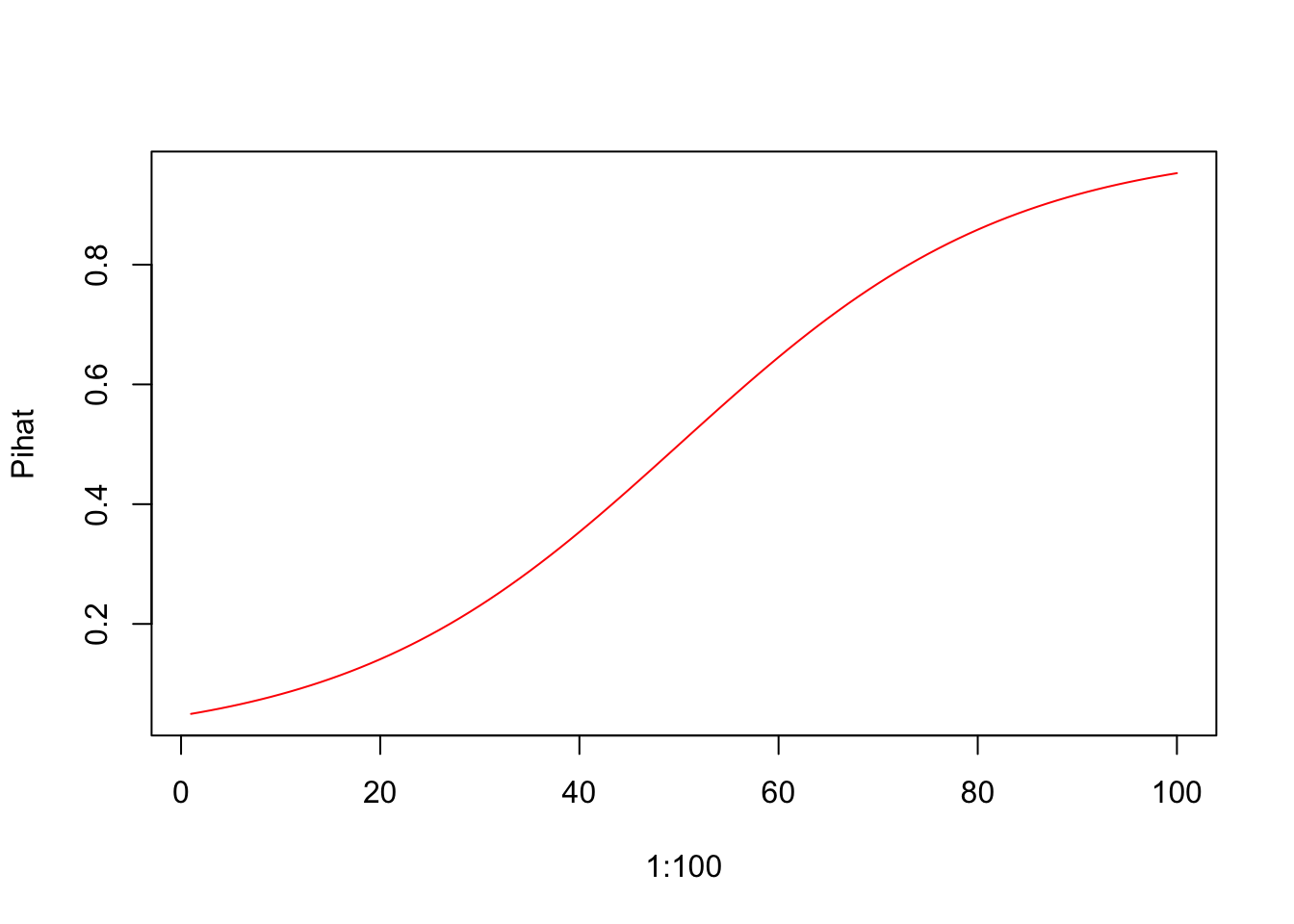

5.0.2 Plots
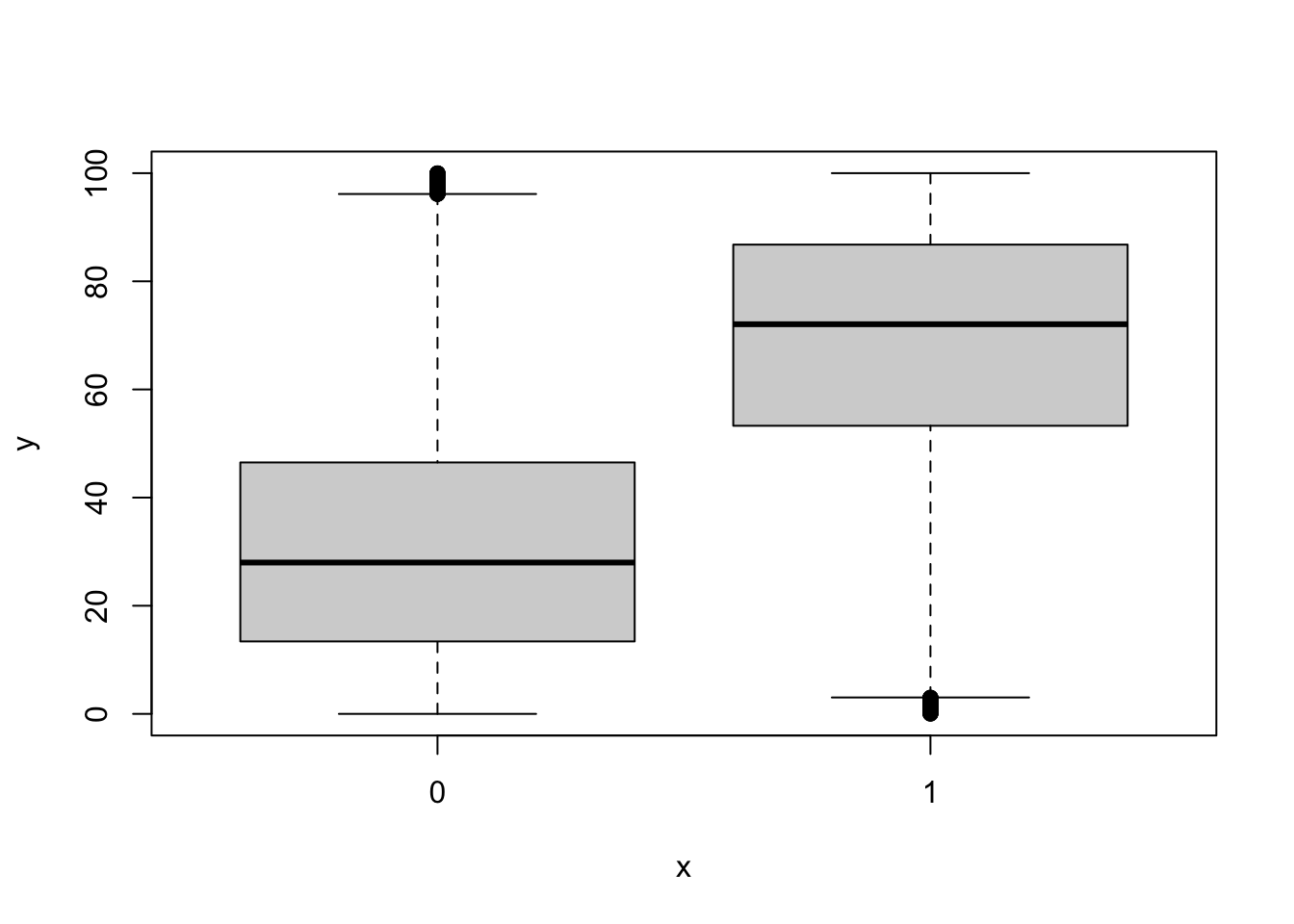
Y vs. X (Not very useful)
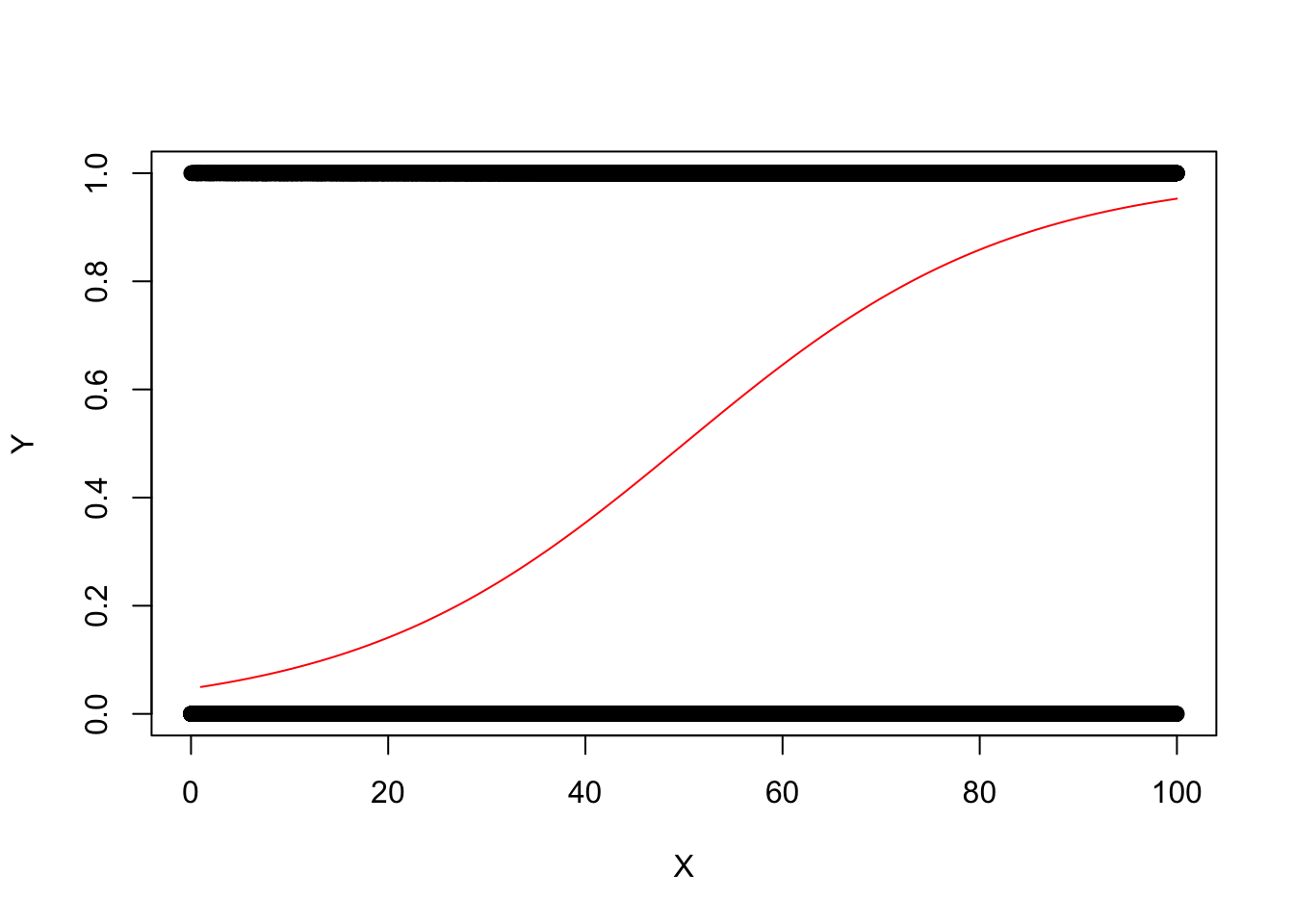
#Grouplot of Pihat vs X
source("http://faculty.tarleton.edu/crawford/documents/math505/LogisticRegressionFunctions.txt")
groupplot.results=groupplot(X,Y,20)
plot(groupplot.results$x,groupplot.results$Pi,
xlab="X",
ylab="Pihat")
lines(1:100,Pihat,col="red")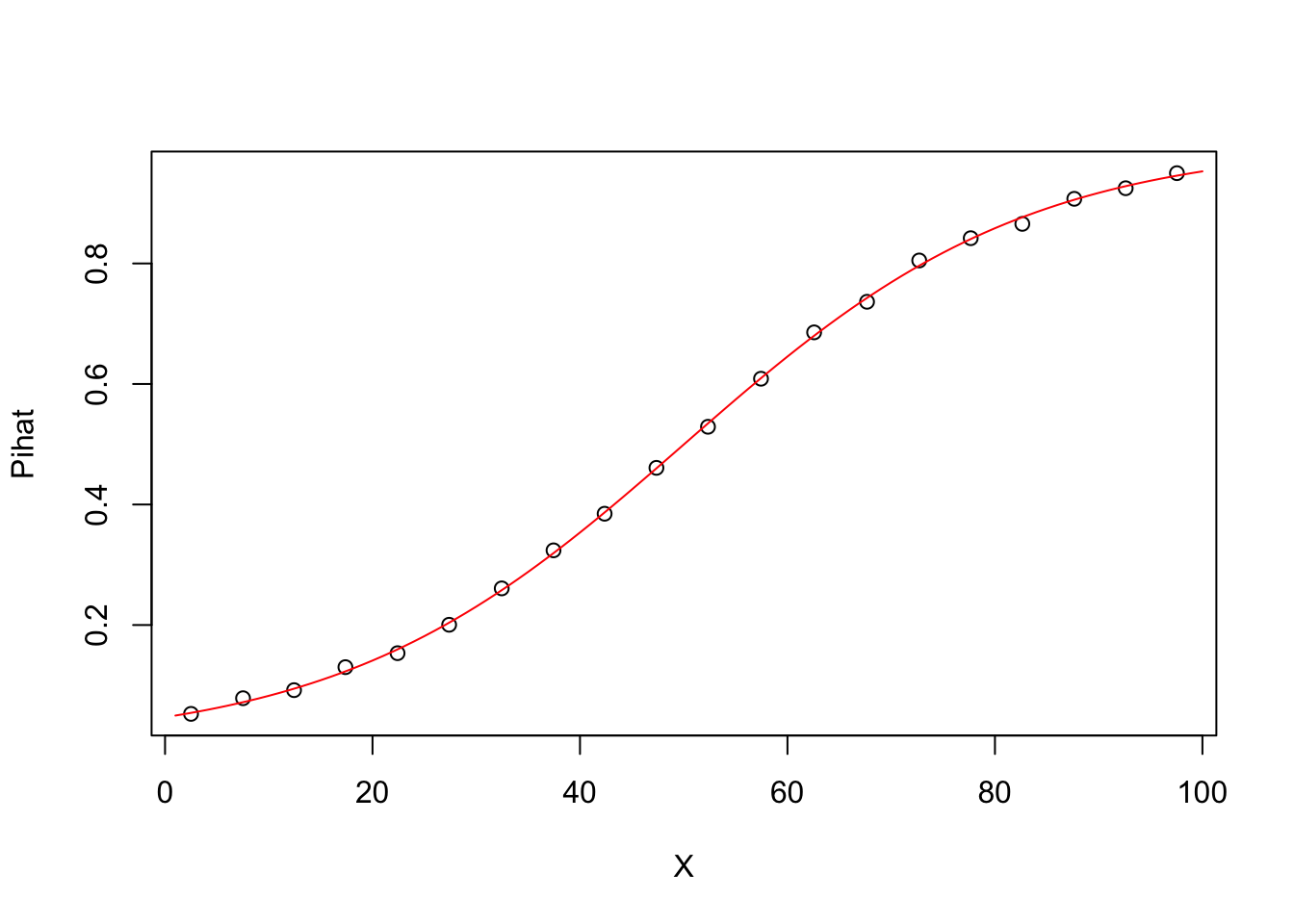
Comments The data set has been broken into 20 groups based on values of X
For each point in the plot, the x-coordinate is the average value of X in that group.
For each point in the plot, the y-coordinate is the proportion of observations in that group where Y=1. In other words, the y-coordinates provide an estimate of Pi = P(Y=1) for each group.
5.0.3 Plot of ghat vs X
group.Pihat=groupplot.results$Pi
group.ghat=log(group.Pihat/(1-group.Pihat))
plot(groupplot.results$x,group.ghat)
lines(1:100,ghat,col="red")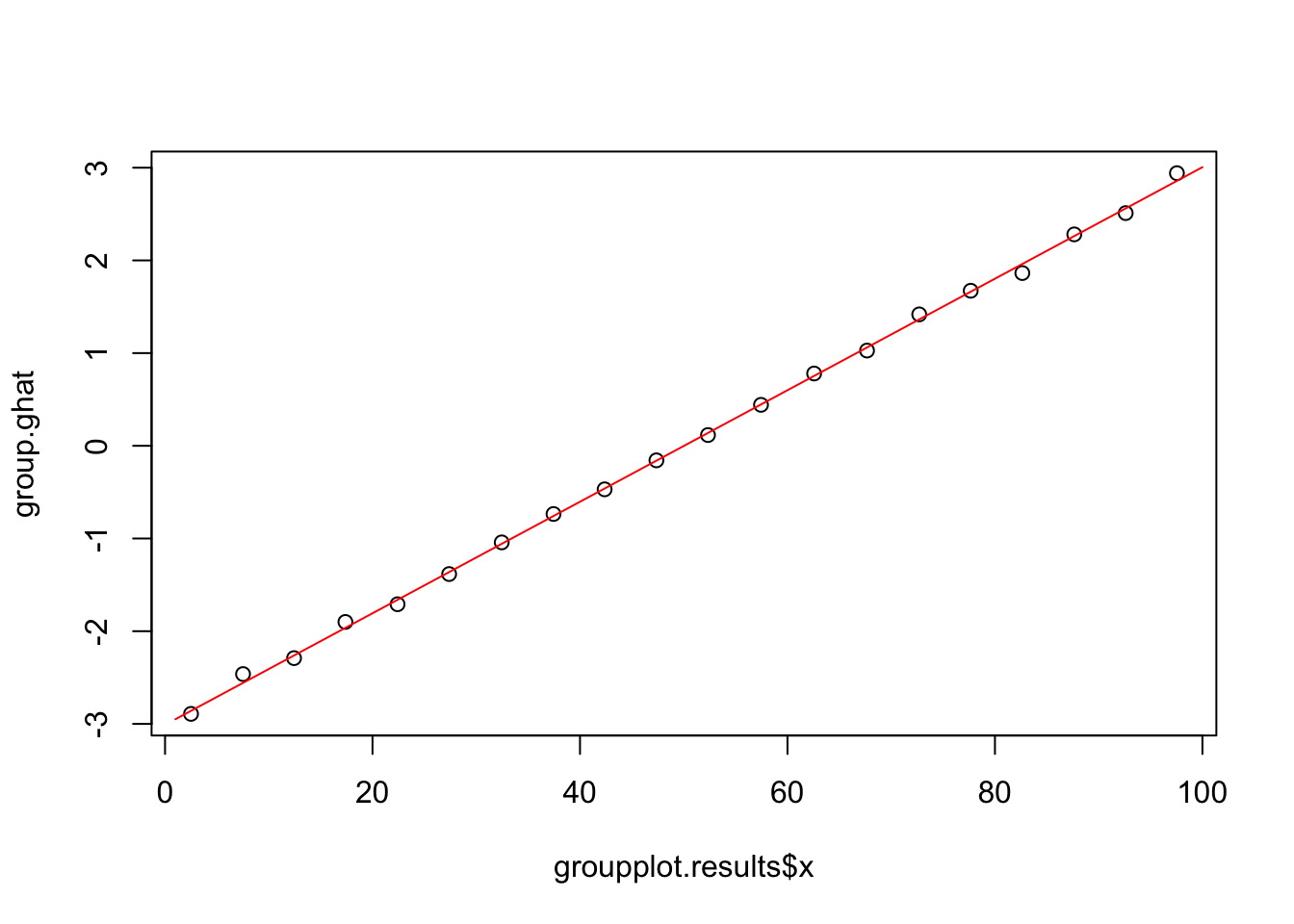
5.0.4 An Example Involving Curvature
set.seed(5366)
X=runif(100000,0,100)
g=-3+.05524*X -.002333*X^2 + .00002381*X^3
Pi=(1/(1+exp(-g)))
U=runif(100000)
Y=(U<Pi) * 1
#Degree 1 model Pihat vs X
model1=glm(Y~X,family=binomial)
summary(model1)##
## Call:
## glm(formula = Y ~ X, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.3886 -0.5858 -0.2904 -0.1404 3.1861
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.0709619 0.0355466 -142.7 <2e-16 ***
## X 0.0555489 0.0004697 118.3 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 92006 on 99999 degrees of freedom
## Residual deviance: 69547 on 99998 degrees of freedom
## AIC: 69551
##
## Number of Fisher Scoring iterations: 6groupplot.results=groupplot(X,Y,20)
plot(groupplot.results$x,groupplot.results$Pi,
xlab="X",
ylab="Pihat")
x.plot.vector=1:100
Pi.plot.vector=predict(model1,
newdata=data.frame(X=x.plot.vector),
type="response")
lines(x.plot.vector,
Pi.plot.vector,
col="red")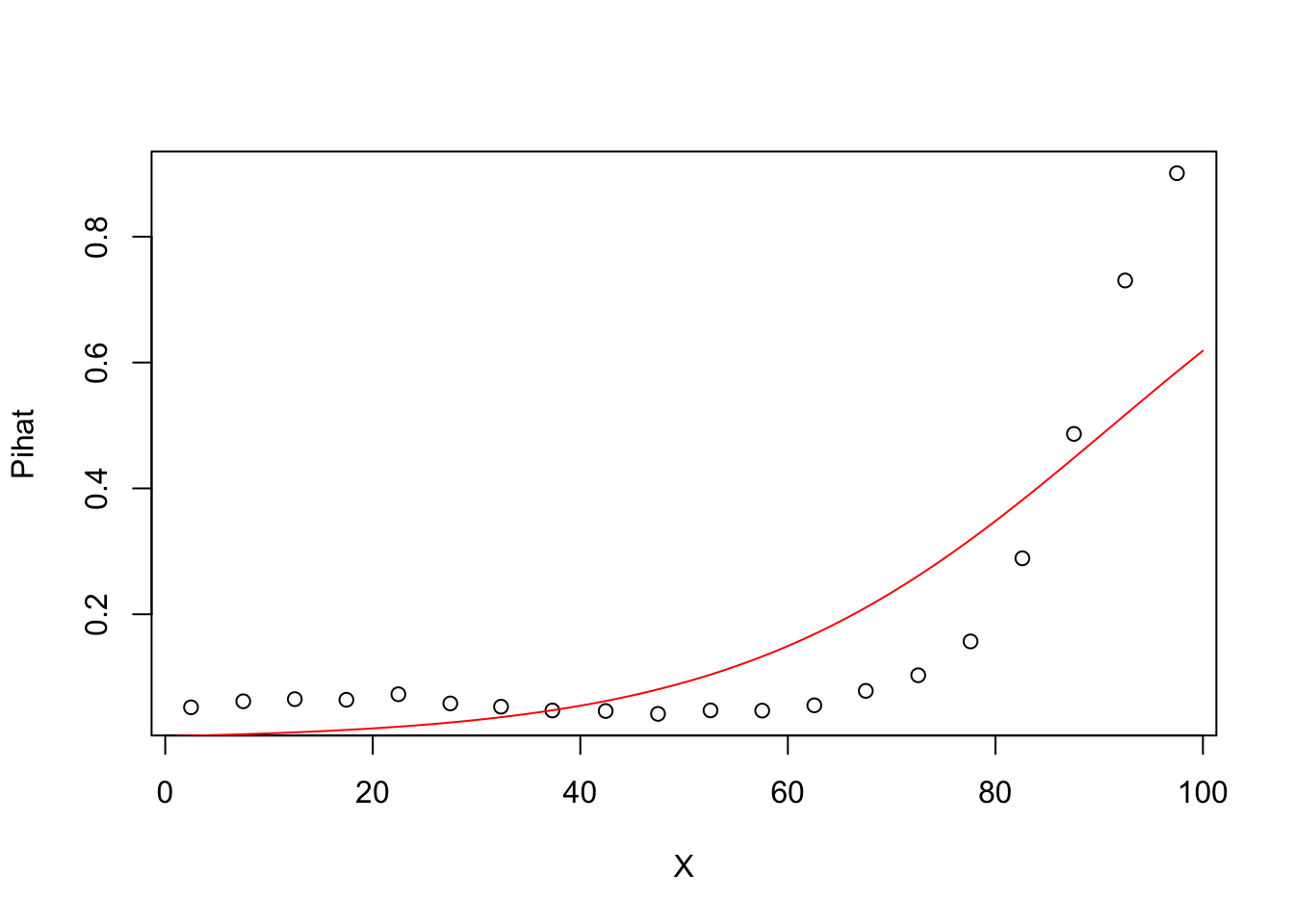
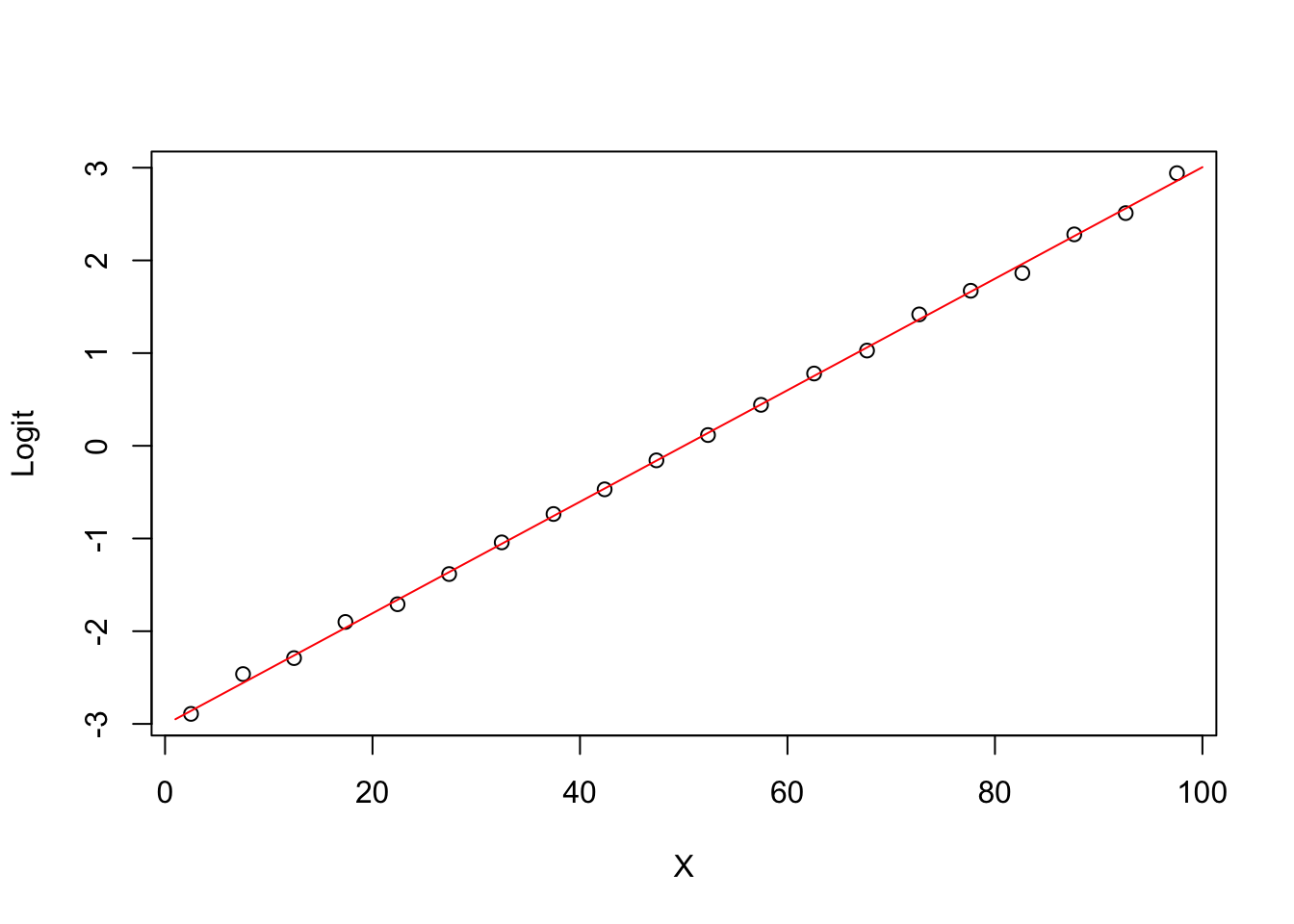
5.0.5 Degree 1 model Logit (ghat) vs X
plot(groupplot.results$x,groupplot.results$g,
xlab="X",
ylab="Logit")
x.plot.vector=1:100
g.plot.vector=predict(model1,
newdata=data.frame(X=x.plot.vector))
lines(x.plot.vector,
g.plot.vector,
col="red")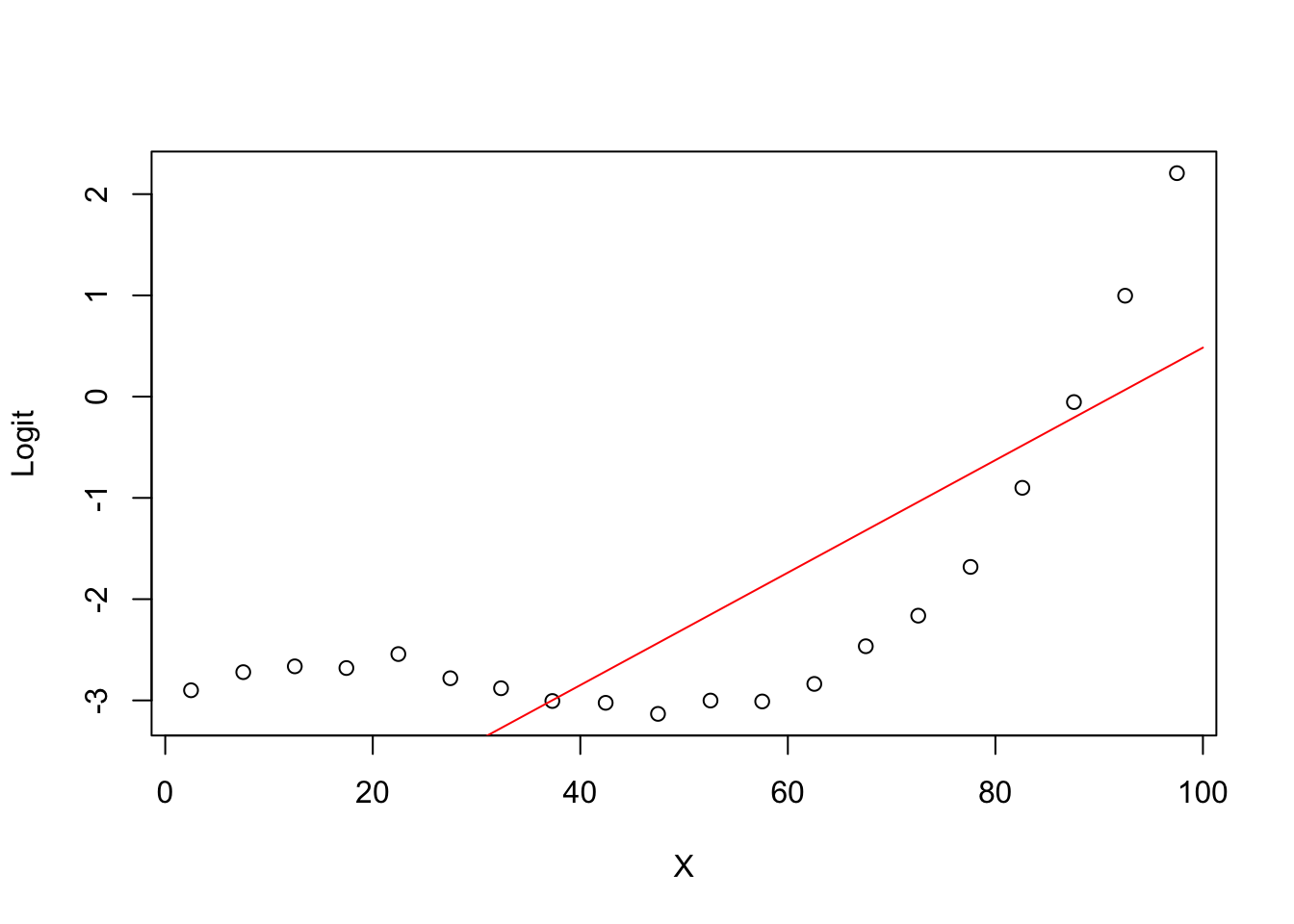
5.0.6 Degree 2 model Pihat vs X
##
## Call:
## glm(formula = Y ~ X + I(X^2), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0622 -0.4332 -0.2843 -0.2347 2.6938
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.797e+00 3.373e-02 -53.27 <2e-16 ***
## X -9.966e-02 1.568e-03 -63.56 <2e-16 ***
## I(X^2) 1.376e-03 1.501e-05 91.67 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 92006 on 99999 degrees of freedom
## Residual deviance: 60972 on 99997 degrees of freedom
## AIC: 60978
##
## Number of Fisher Scoring iterations: 5groupplot.results=groupplot(X,Y,20)
plot(groupplot.results$x,groupplot.results$Pi,
xlab="X",
ylab="Pihat")
x.plot.vector=1:100
Pi.plot.vector=predict(model2,
newdata=data.frame(X=x.plot.vector),
type="response")
lines(x.plot.vector,
Pi.plot.vector,
col="red")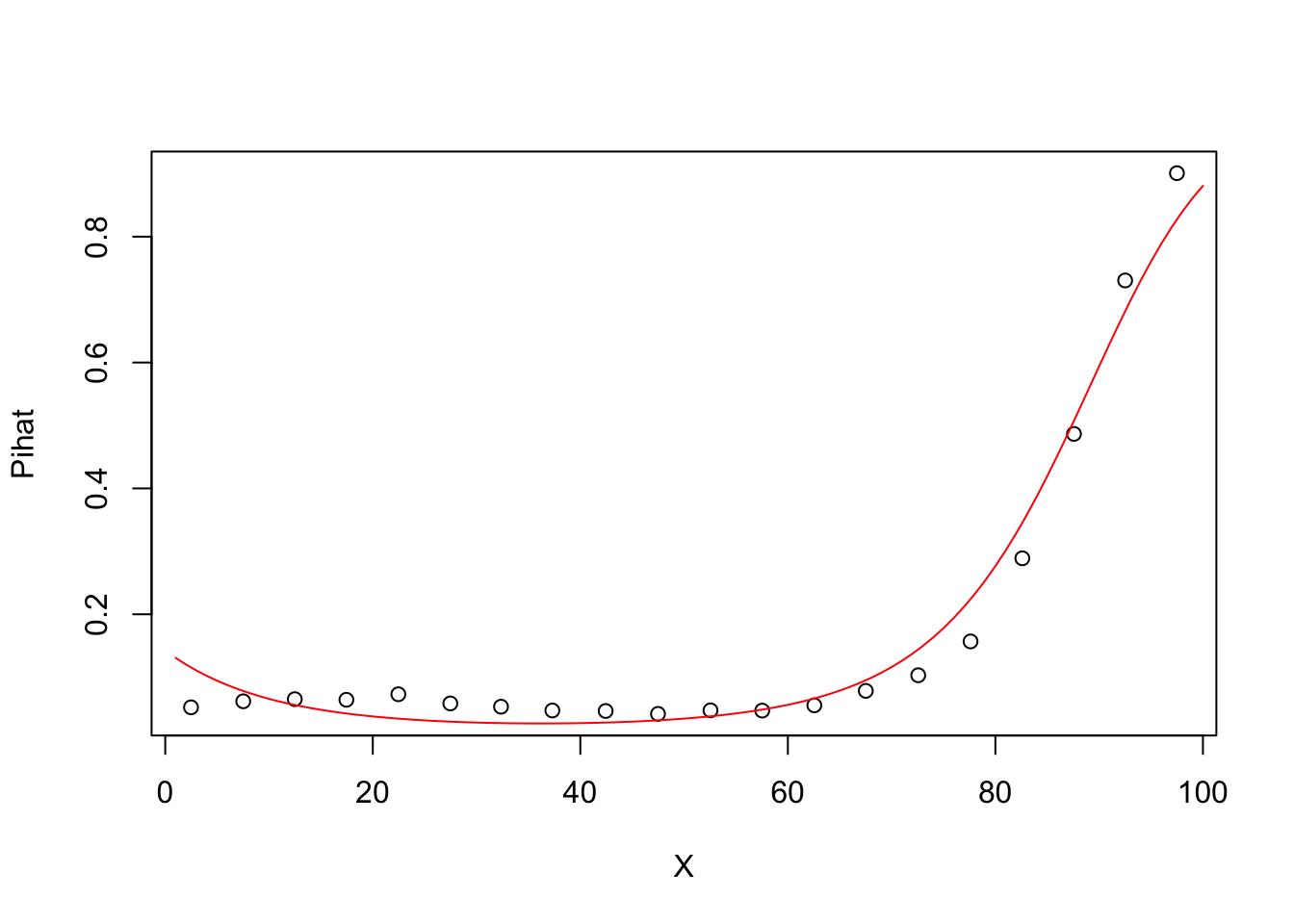
5.0.7 Degree 2 model Logit (ghat) vs X
plot(groupplot.results$x,groupplot.results$g,
xlab="X",
ylab="Logit")
x.plot.vector=1:100
g.plot.vector=predict(model2,
newdata=data.frame(X=x.plot.vector))
lines(x.plot.vector,
g.plot.vector,
col="red")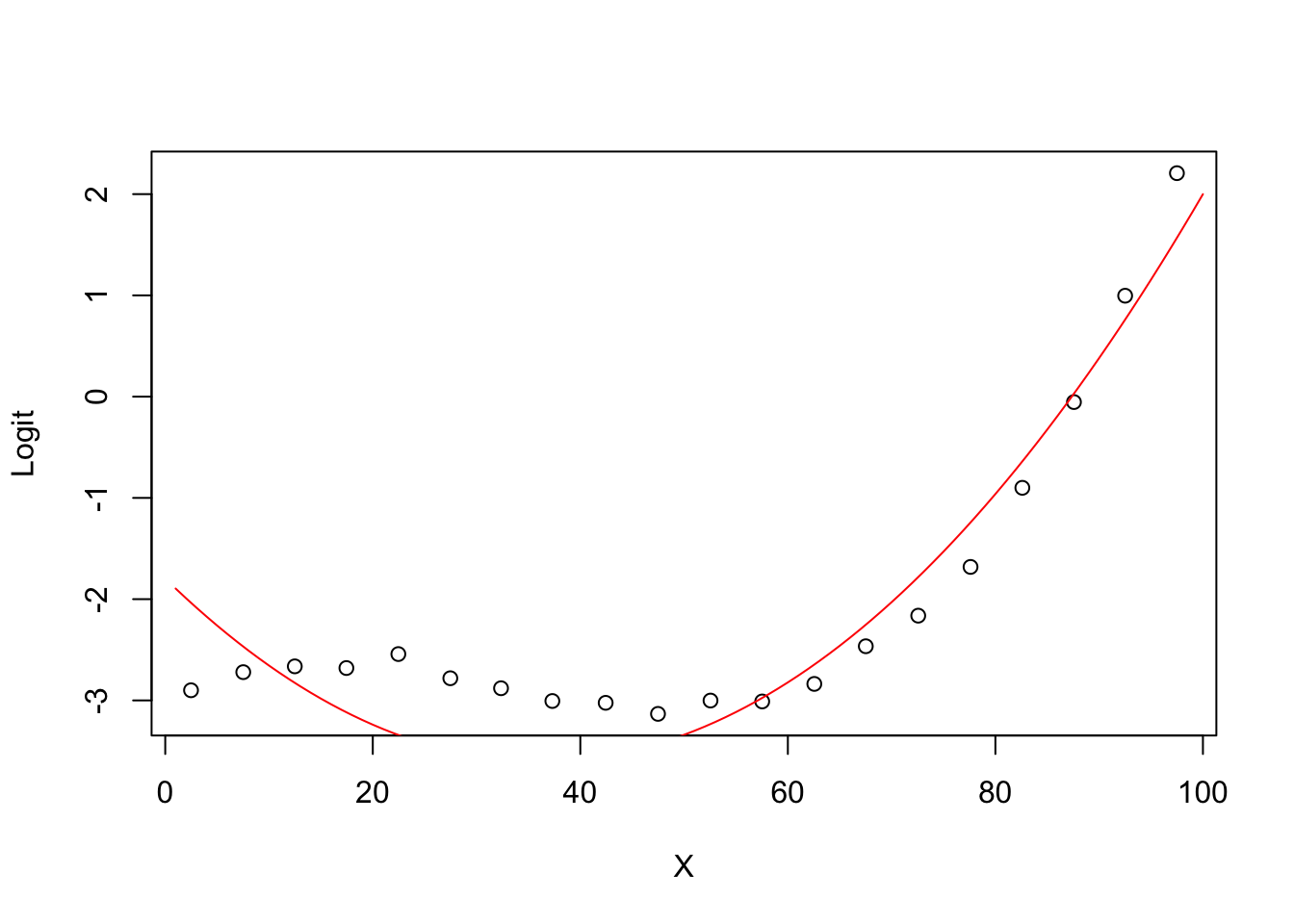
5.0.8 Degree 3 model Pihat vs X
##
## Call:
## glm(formula = Y ~ X + I(X^2) + I(X^3), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4714 -0.3712 -0.3361 -0.3006 2.5057
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.026e+00 5.438e-02 -55.65 <2e-16 ***
## X 5.595e-02 4.523e-03 12.37 <2e-16 ***
## I(X^2) -2.336e-03 9.953e-05 -23.48 <2e-16 ***
## I(X^3) 2.380e-05 6.321e-07 37.65 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 92006 on 99999 degrees of freedom
## Residual deviance: 59457 on 99996 degrees of freedom
## AIC: 59465
##
## Number of Fisher Scoring iterations: 5groupplot.results=groupplot(X,Y,20)
plot(groupplot.results$x,groupplot.results$Pi,
xlab="X",
ylab="Pihat")
x.plot.vector=1:100
Pi.plot.vector=predict(model3,
newdata=data.frame(X=x.plot.vector),
type="response")
lines(x.plot.vector,
Pi.plot.vector,
col="red")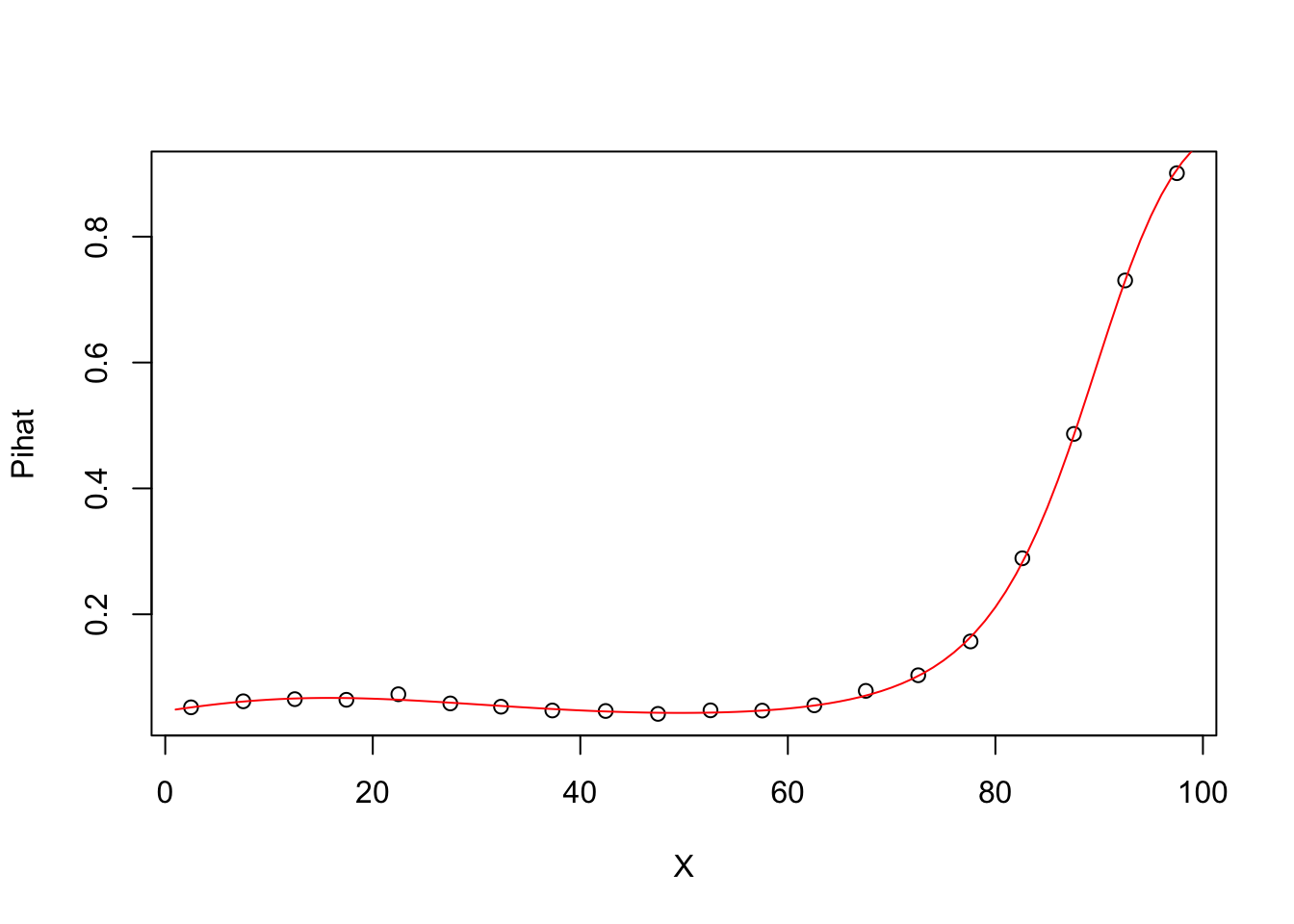
5.0.9 Degree 3 model Logit (ghat) vs X
plot(groupplot.results$x,groupplot.results$g,
xlab="X",
ylab="Logit")
x.plot.vector=1:100
g.plot.vector=predict(model3,
newdata=data.frame(X=x.plot.vector))
lines(x.plot.vector,
g.plot.vector,
col="red")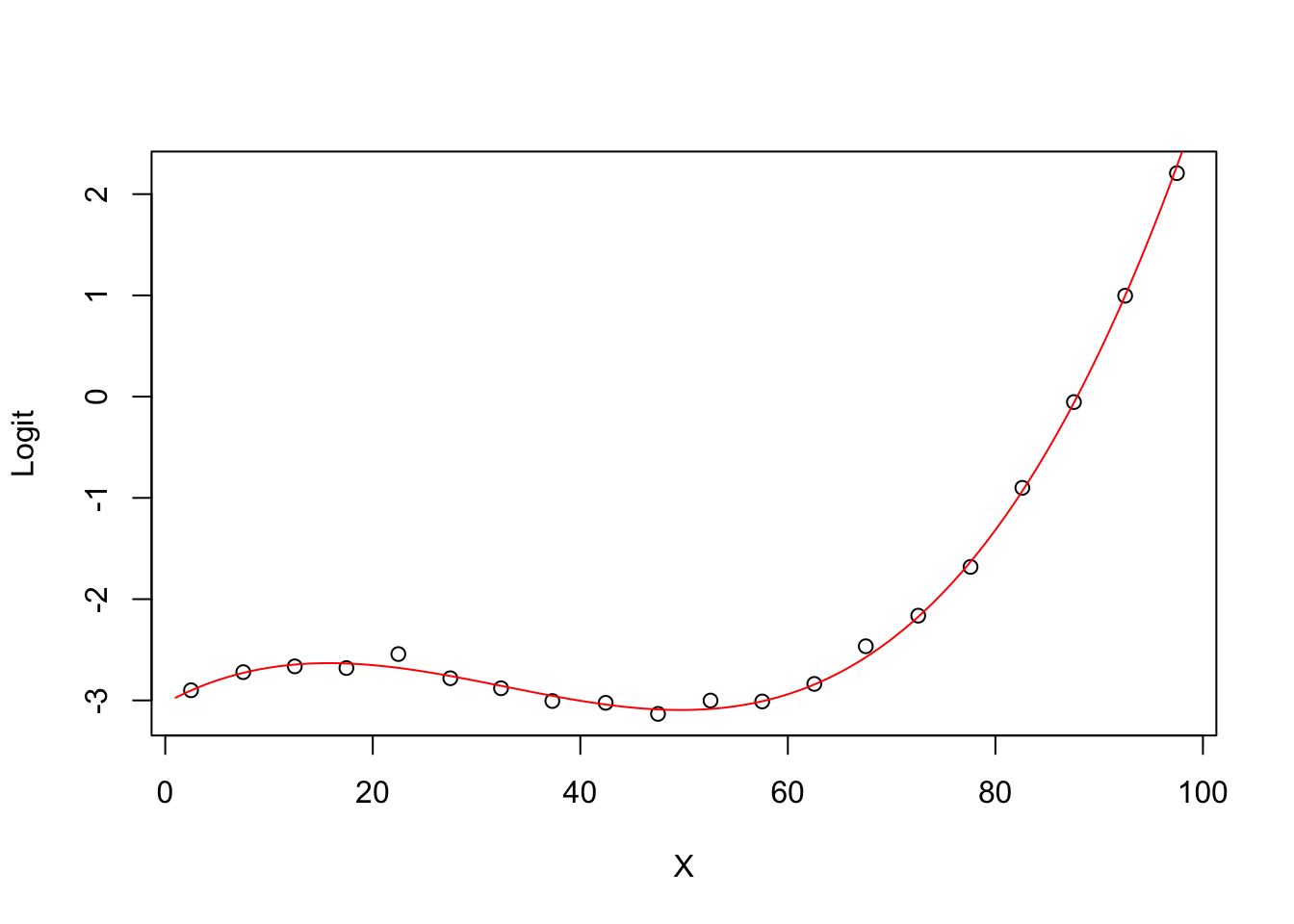
5.0.10 Degree 4 model Pihat vs X
##
## Call:
## glm(formula = Y ~ X + I(X^2) + I(X^3) + I(X^4), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4759 -0.3704 -0.3365 -0.3013 2.5035
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.012e+00 6.906e-02 -43.615 < 2e-16 ***
## X 5.330e-02 9.144e-03 5.829 5.58e-09 ***
## I(X^2) -2.221e-03 3.595e-04 -6.179 6.44e-10 ***
## I(X^3) 2.207e-05 5.239e-06 4.212 2.53e-05 ***
## I(X^4) 8.449e-09 2.534e-08 0.333 0.739
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 92006 on 99999 degrees of freedom
## Residual deviance: 59457 on 99995 degrees of freedom
## AIC: 59467
##
## Number of Fisher Scoring iterations: 5groupplot.results=groupplot(X,Y,20)
plot(groupplot.results$x,groupplot.results$Pi,
xlab="X",
ylab="Pihat")
x.plot.vector=1:100
Pi.plot.vector=predict(model4,
newdata=data.frame(X=x.plot.vector),
type="response")
lines(x.plot.vector,
Pi.plot.vector,
col="red")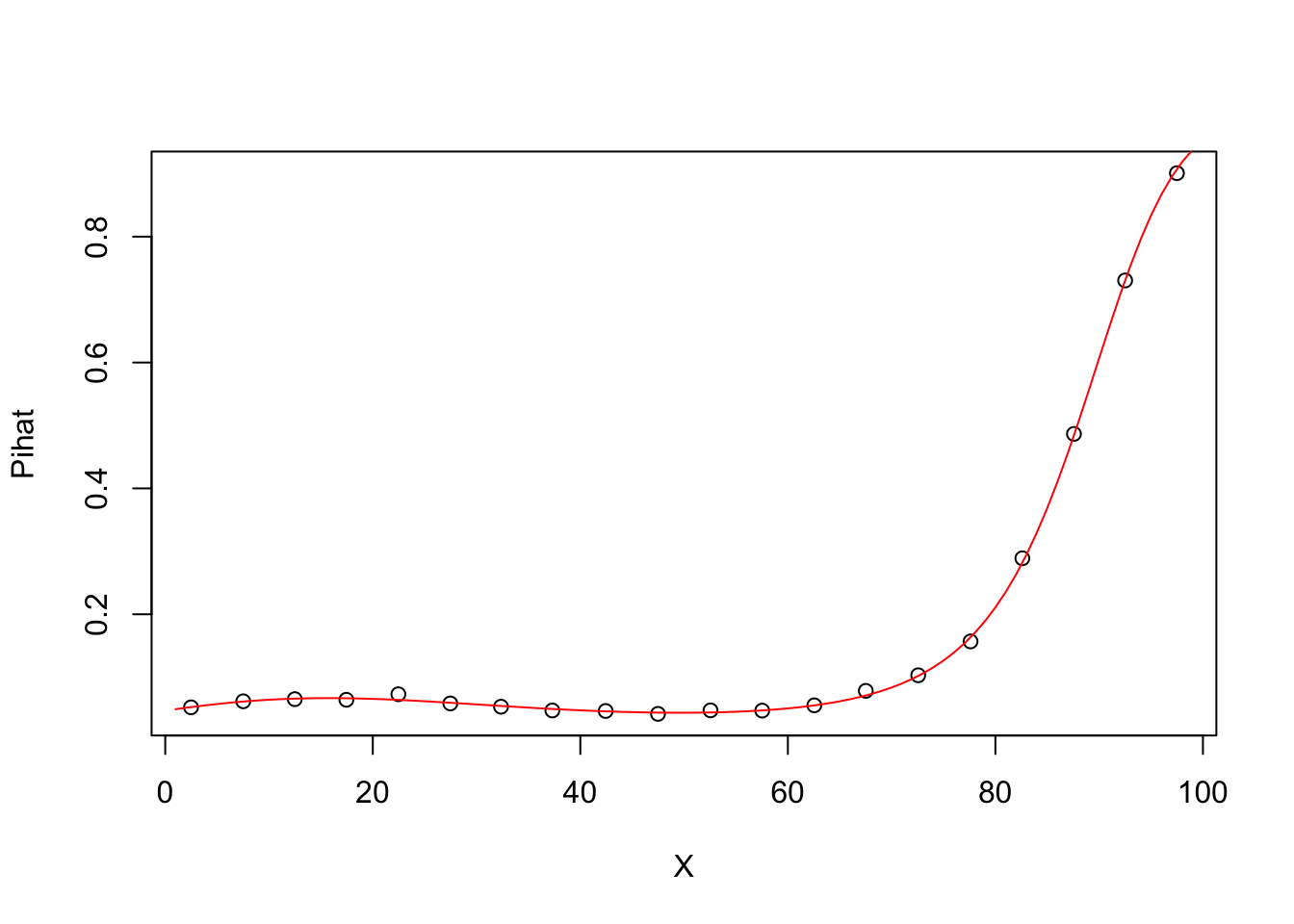
5.0.11 Degree 4 model Logit (ghat) vs X
plot(groupplot.results$x,groupplot.results$g,
xlab="X",
ylab="Logit")
x.plot.vector=1:100
g.plot.vector=predict(model4,
newdata=data.frame(X=x.plot.vector))
lines(x.plot.vector,
g.plot.vector,
col="red")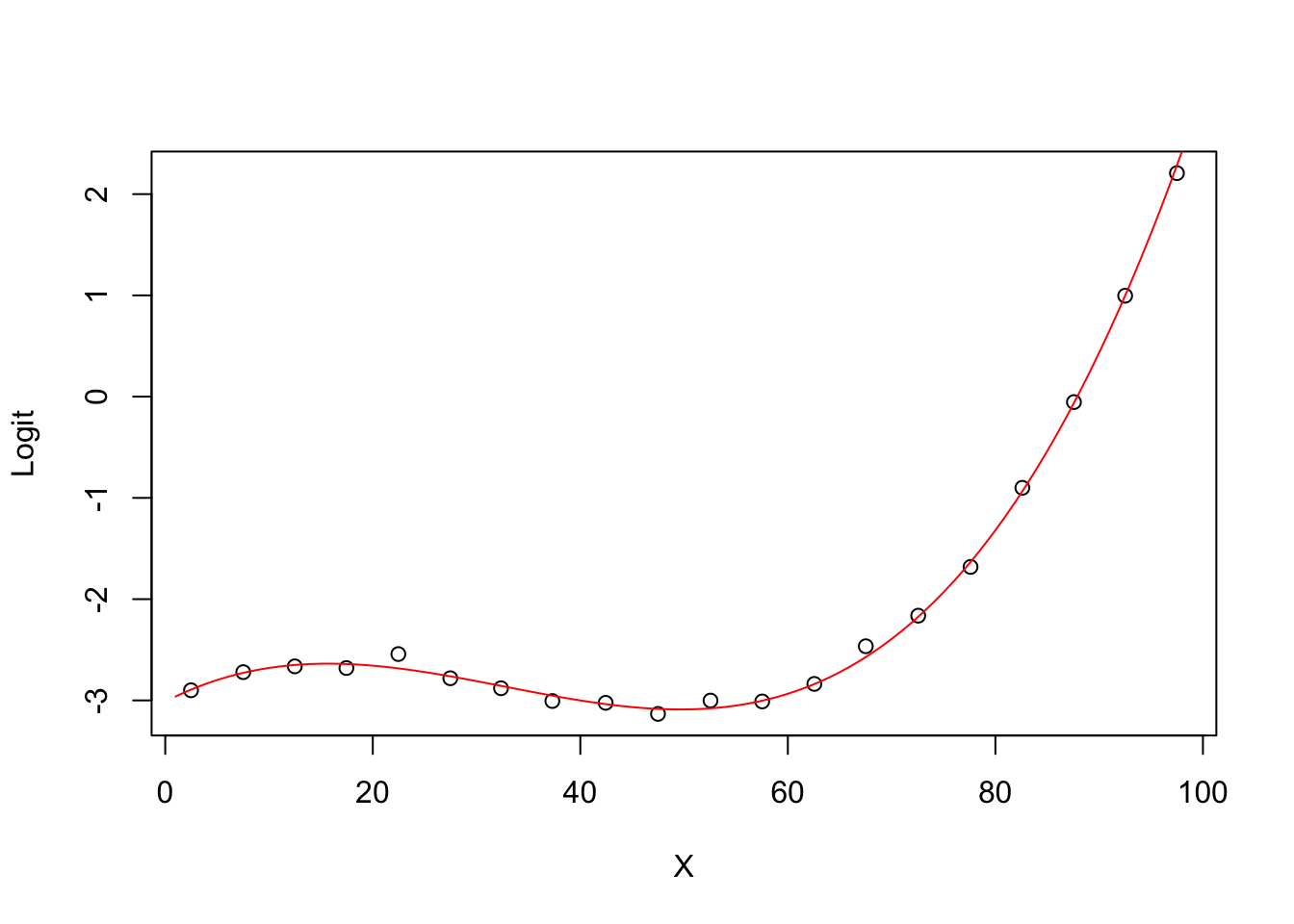
5.1 Testing model1 vs model3
G=model1$deviance-model3$deviance
pchisq(G,lower.tail=FALSE,df=model1$df.residual-model2$df.residual)## [1] 0## [1] 0## [1] 0.73880445.2 A Multivariate Example
set.seed(5366)
Rank=rnorm(200,.67,.1)
SAT=round(rnorm(200,980,132),-1)
ShoeSize=round(rnorm(200,9,1),1)
U=runif(200,0,1)
Mother=1:200
for(i in 1:200){
if(U[i]<.5){Mother[i]="SomeCollege"}
if((U[i]>.5)&(U[i]<.8)){Mother[i]="Bachelors"}
if((U[i]>.8)&(U[i]<.95)){Mother[i]="HighSchool"}
if(U[i]>0.95){Mother[i]="GradDegree"}
}
Mother=as.factor(Mother)
Mother=relevel(Mother,4)
tempmodel=lm(1:200~Rank+SAT+Mother)
X=model.matrix(tempmodel)
beta=c(-9.3,10,.00364,1.5,1.5,0)
g=X%*%beta
Pi=1/(1+exp(-g))
U2=runif(200,0,1)
Retention=(U2<Pi)*1
Retention.data=data.frame(Rank,SAT,ShoeSize,Mother)
#Fitting a model
model=glm(Retention~.,data=Retention.data,family=binomial)
summary(model)##
## Call:
## glm(formula = Retention ~ ., family = binomial, data = Retention.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7118 0.1951 0.3948 0.6374 1.3498
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.293975 3.095703 -2.679 0.007380 **
## Rank 10.277291 2.467877 4.164 3.12e-05 ***
## SAT 0.004871 0.001576 3.090 0.002002 **
## ShoeSize -0.233967 0.207032 -1.130 0.258435
## MotherBachelors 1.927406 0.555780 3.468 0.000524 ***
## MotherGradDegree 0.882259 1.180404 0.747 0.454809
## MotherHighSchool -0.028233 0.514632 -0.055 0.956249
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 156.62 on 193 degrees of freedom
## AIC: 170.62
##
## Number of Fisher Scoring iterations: 5Better Plotting Function
quantlogitplot=function(Y,x,degree,xname,Yname,numgroups,yrange){
xrange=range(x)
n=length(Y)
X=rep(1,n)
for(i in 1:degree){
X=cbind(X,x^i)
}
model=glm(Y~X-1,family='binomial')
L=groupplot(x,Y,numgroups)
plot(L$x,L$g,xlab=xname,ylab=Yname,ylim=yrange)
a=xrange[1]
b=xrange[2]
index=(1:100)/100
index=a+(b-a)*index
Index=rep(1,100)
for(i in 1:degree){
Index=cbind(Index,index^i)
}
betahat=coef(model)
lines(index,Index%*%betahat,col='red')
}Rank model
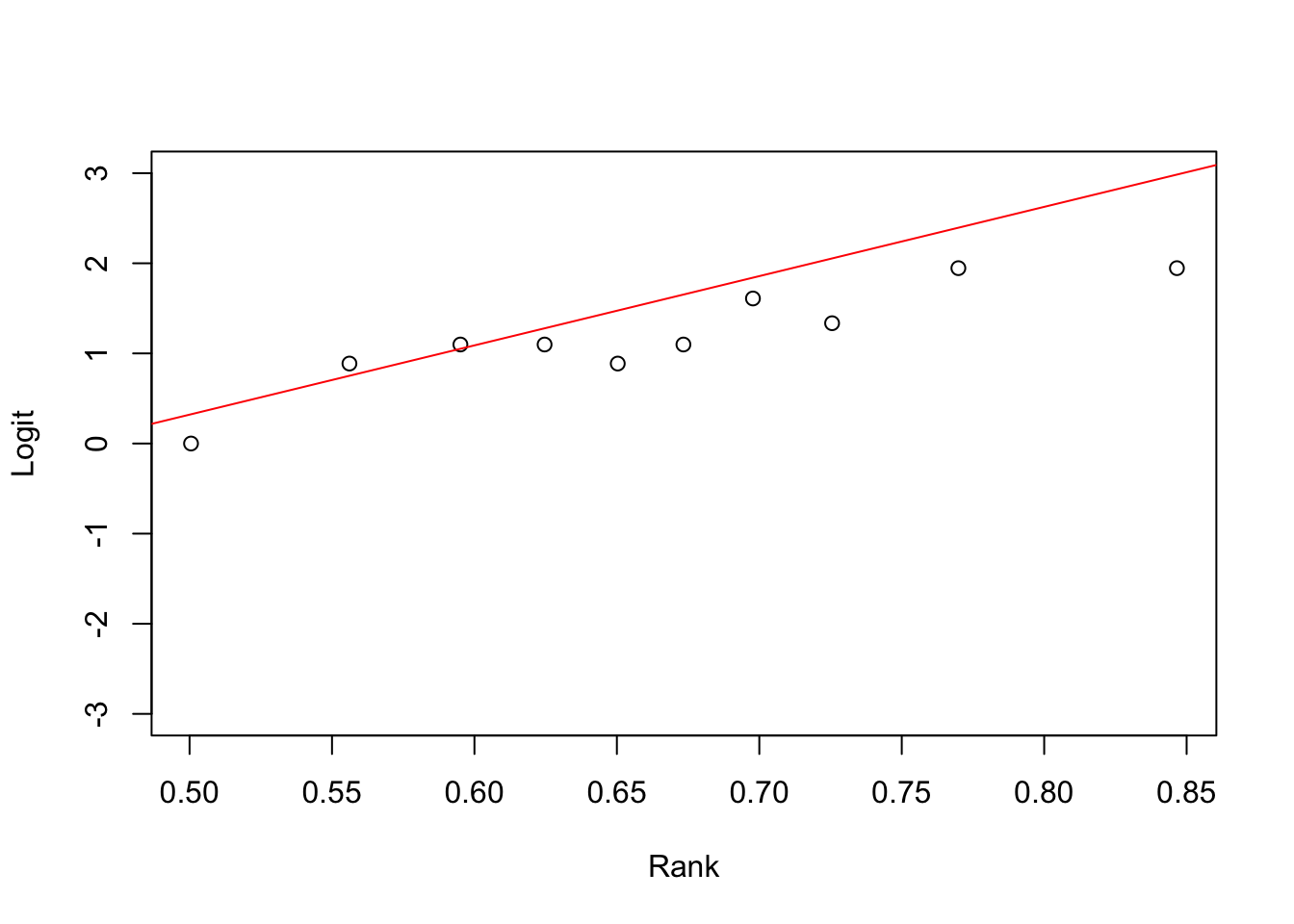
rank.model=glm(Retention~Rank,family=binomial)
rank.model.2=glm(Retention~Rank+I(Rank^2),family=binomial)
summary(rank.model)##
## Call:
## glm(formula = Retention ~ Rank, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6285 0.3307 0.5337 0.7007 1.1764
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.522 1.339 -2.631 0.008505 **
## Rank 7.685 2.124 3.619 0.000296 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 182.27 on 198 degrees of freedom
## AIC: 186.27
##
## Number of Fisher Scoring iterations: 5##
## Call:
## glm(formula = Retention ~ Rank + I(Rank^2), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4764 0.3629 0.5269 0.6848 1.2464
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -6.161 7.049 -0.874 0.382
## Rank 16.100 22.111 0.728 0.467
## I(Rank^2) -6.574 17.137 -0.384 0.701
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 182.12 on 197 degrees of freedom
## AIC: 188.12
##
## Number of Fisher Scoring iterations: 5## [1] 0.7062637SAT model

SAT.model=glm(Retention~SAT,family=binomial)
SAT.model.2=glm(Retention~SAT+I(SAT^2),family=binomial)
summary(SAT.model)##
## Call:
## glm(formula = Retention ~ SAT, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1306 0.4343 0.5911 0.7097 1.0585
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.020442 1.342033 -1.506 0.1322
## SAT 0.003604 0.001422 2.534 0.0113 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 190.36 on 198 degrees of freedom
## AIC: 194.36
##
## Number of Fisher Scoring iterations: 4##
## Call:
## glm(formula = Retention ~ SAT + I(SAT^2), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1492 0.4182 0.5974 0.7177 0.9973
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.841e-01 7.425e+00 -0.052 0.959
## SAT 1.239e-04 1.561e-02 0.008 0.994
## I(SAT^2) 1.817e-06 8.128e-06 0.224 0.823
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 190.31 on 197 degrees of freedom
## AIC: 196.31
##
## Number of Fisher Scoring iterations: 5## [1] 0.821137Shoe Size model
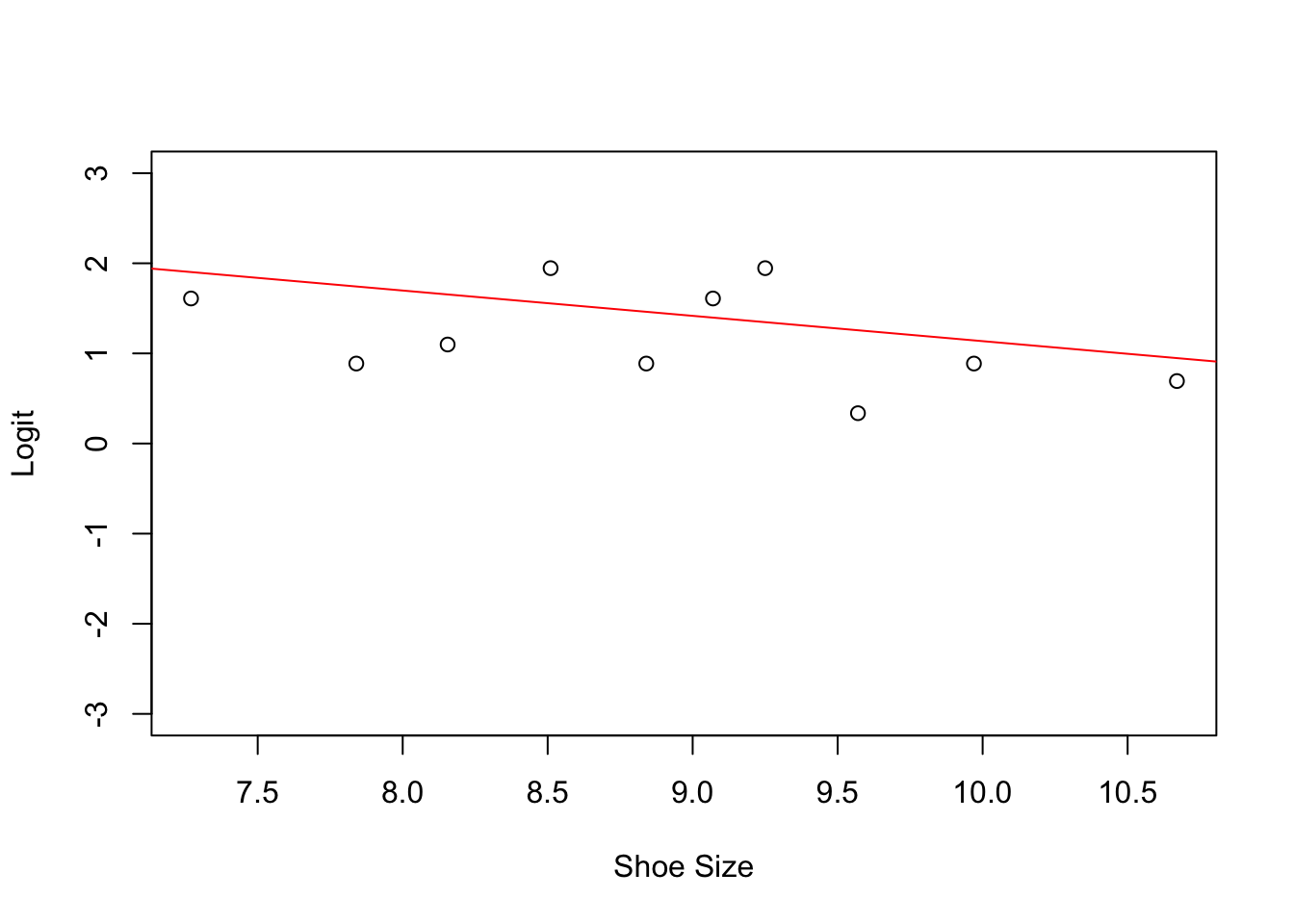
##
## Call:
## glm(formula = Retention ~ ShoeSize, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0653 0.5434 0.6263 0.6758 0.8619
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.9444 1.6823 2.345 0.019 *
## ShoeSize -0.2808 0.1843 -1.524 0.128
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 195.00 on 198 degrees of freedom
## AIC: 199
##
## Number of Fisher Scoring iterations: 4Mother’s Education Level
## Mother
## SomeCollege Bachelors GradDegree HighSchool
## 89 71 6 34##
## Call:
## glm(formula = Retention ~ ., family = binomial, data = Retention.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.7118 0.1951 0.3948 0.6374 1.3498
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.293975 3.095703 -2.679 0.007380 **
## Rank 10.277291 2.467877 4.164 3.12e-05 ***
## SAT 0.004871 0.001576 3.090 0.002002 **
## ShoeSize -0.233967 0.207032 -1.130 0.258435
## MotherBachelors 1.927406 0.555780 3.468 0.000524 ***
## MotherGradDegree 0.882259 1.180404 0.747 0.454809
## MotherHighSchool -0.028233 0.514632 -0.055 0.956249
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 156.62 on 193 degrees of freedom
## AIC: 170.62
##
## Number of Fisher Scoring iterations: 5##
## Call:
## glm(formula = Retention ~ Rank + SAT + ShoeSize, family = binomial,
## data = Retention.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.3186 0.2787 0.4652 0.6840 1.3253
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.576068 2.787273 -2.001 0.045441 *
## Rank 7.552550 2.170519 3.480 0.000502 ***
## SAT 0.003959 0.001482 2.670 0.007580 **
## ShoeSize -0.182597 0.195038 -0.936 0.349163
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 173.74 on 196 degrees of freedom
## AIC: 181.74
##
## Number of Fisher Scoring iterations: 5## [1] 0.0006693412Recoding Mother’s Education Level
## Mother
## SomeCollege Bachelors GradDegree HighSchool
## 89 71 6 34##
## 1 2 3 4
## 89 71 6 34Mother.Recode=c("HighSchool/SomeCollege",
"Bachelors/GradDegree",
"Bachelors/GradDegree",
"HighSchool/SomeCollege"
)
Mother2=Mother.Recode[Mother]
table(Mother2)## Mother2
## Bachelors/GradDegree HighSchool/SomeCollege
## 77 123##
## Call:
## glm(formula = Retention ~ Rank + SAT + ShoeSize + Mother2, family = binomial,
## data = Retention.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6724 0.2069 0.4023 0.6406 1.3438
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -6.339209 2.964094 -2.139 0.03246 *
## Rank 10.073942 2.417513 4.167 3.09e-05 ***
## SAT 0.004881 0.001572 3.104 0.00191 **
## ShoeSize -0.235572 0.206512 -1.141 0.25399
## Mother2HighSchool/SomeCollege -1.827392 0.500327 -3.652 0.00026 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 157.24 on 195 degrees of freedom
## AIC: 167.24
##
## Number of Fisher Scoring iterations: 5## [1] 0.7323225Removing Shoe Size
##
## Call:
## glm(formula = Retention ~ Rank + SAT + Mother2, family = binomial,
## data = Retention.data)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6402 0.2009 0.4144 0.6228 1.3829
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.683127 2.187868 -3.969 7.22e-05 ***
## Rank 10.436952 2.409344 4.332 1.48e-05 ***
## SAT 0.004852 0.001561 3.107 0.001887 **
## Mother2HighSchool/SomeCollege -1.793748 0.496847 -3.610 0.000306 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 158.57 on 196 degrees of freedom
## AIC: 166.57
##
## Number of Fisher Scoring iterations: 5## [1] 0.5841335.2.1 Variable Selection
Stepwise
## Start: AIC=170.62
## Retention ~ Rank + SAT + ShoeSize + Mother
##
## Df Deviance AIC
## - ShoeSize 1 157.92 169.92
## <none> 156.62 170.62
## - SAT 1 167.33 179.33
## - Mother 3 173.74 181.74
## - Rank 1 178.21 190.21
##
## Step: AIC=169.92
## Retention ~ Rank + SAT + Mother
##
## Df Deviance AIC
## <none> 157.92 169.92
## - SAT 1 168.57 178.57
## - Mother 3 174.62 180.62
## - Rank 1 181.53 191.53#Best Subsets
library(bestglm)
X=model.matrix(model)
X=X[,2:(ncol(X))]
y=Retention
Xy=data.frame(X,y)
best.model=bestglm(Xy,family=binomial)## Morgan-Tatar search since family is non-gaussian.## [1] "BestModel" "BestModels" "Bestq" "qTable" "Subsets" "Title"
## [7] "ModelReport"##
## Call:
## glm(formula = y ~ ., family = family, data = Xi, weights = weights)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.6715 0.1966 0.4066 0.6264 1.3696
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -10.429845 2.332693 -4.471 7.78e-06 ***
## Rank 10.610051 2.447711 4.335 1.46e-05 ***
## SAT 0.004724 0.001547 3.054 0.002257 **
## MotherBachelors 1.857860 0.518495 3.583 0.000339 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 197.36 on 199 degrees of freedom
## Residual deviance: 158.45 on 196 degrees of freedom
## AIC: 166.45
##
## Number of Fisher Scoring iterations: 55.3 Assessing Model Performance and Fit
source("http://faculty.tarleton.edu/crawford/documents/Math5364/MiscRFunctions.txt")
#Training Data
Retention.data.2=data.frame(Retention,Rank,SAT,Mother2)
train=trainsample(Retention.data.2,0.7)
#Fitting Model
model=glm(Retention~.,
data=Retention.data.2[train,],
family=binomial)
summary(model)##
## Call:
## glm(formula = Retention ~ ., family = binomial, data = Retention.data.2[train,
## ])
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.4849 0.1980 0.4345 0.6524 1.3690
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -9.168525 2.582276 -3.551 0.000384 ***
## Rank 10.491690 2.887293 3.634 0.000279 ***
## SAT 0.005166 0.001989 2.597 0.009392 **
## Mother2HighSchool/SomeCollege -1.734604 0.581591 -2.983 0.002859 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 142.84 on 139 degrees of freedom
## Residual deviance: 115.67 on 136 degrees of freedom
## AIC: 123.67
##
## Number of Fisher Scoring iterations: 5Classification Accuracy
#confmatrix function from previous tutorial
confmatrix=function(y,predy){
matrix=table(y,predy)
accuracy=sum(diag(matrix))/sum(matrix)
return(list(matrix=matrix,accuracy=accuracy,error=1-accuracy))
}
Pihat=predict(model,
newdata=Retention.data.2[-train,],
type="response")
pred.retention=(Pihat>=0.5)*1
table(pred.retention)## pred.retention
## 0 1
## 8 52## $matrix
## predy
## y 0 1
## 0 5 5
## 1 3 47
##
## $accuracy
## [1] 0.8666667
##
## $error
## [1] 0.1333333ROC Curve
## Setting levels: control = 0, case = 1## Setting direction: controls < cases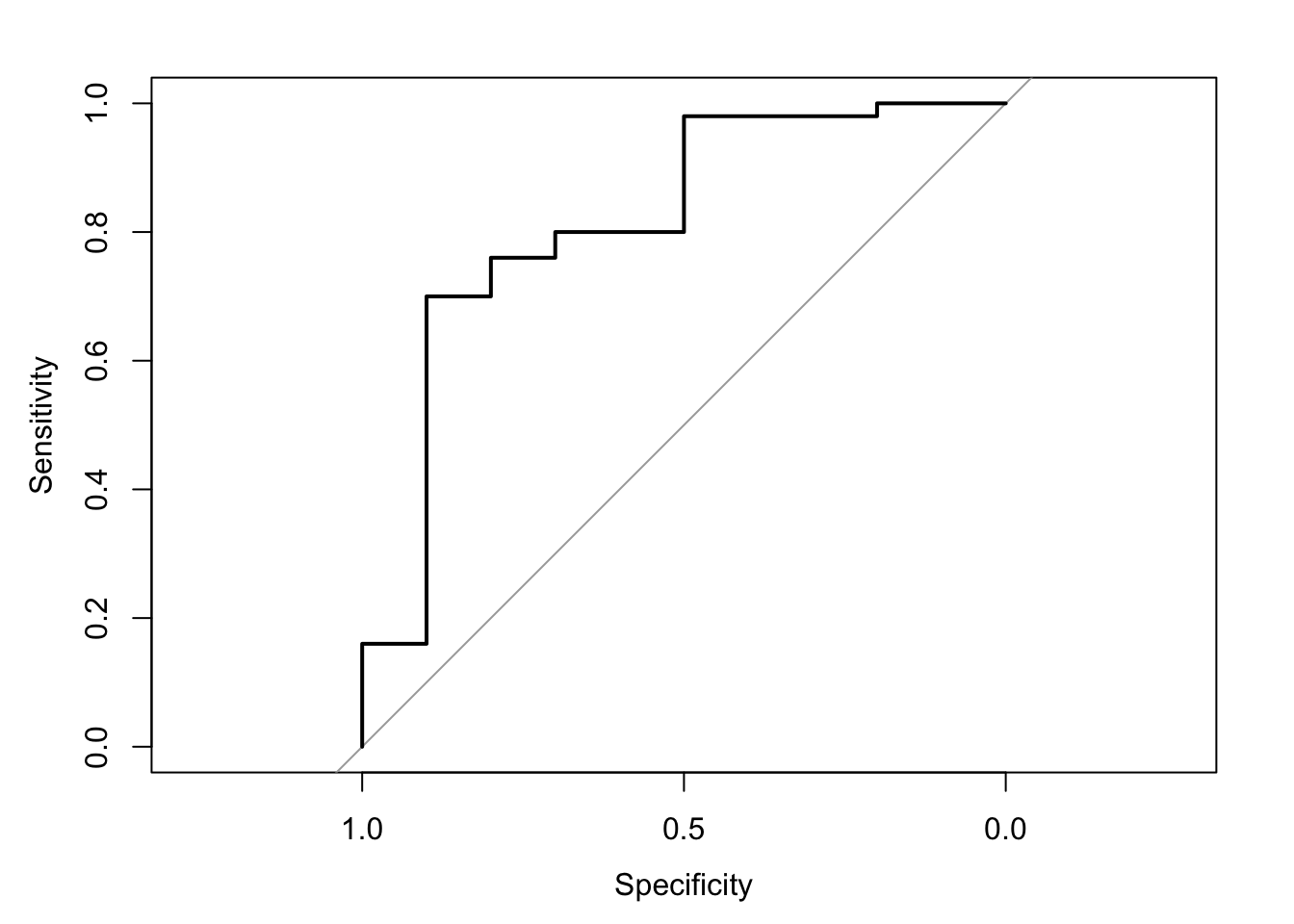
Hosmer-Lemeshow Goodness-of-fit Test
# dependecy doesnt exist cant use
# Hosmer-Lemeshow goodness of fit tests from this package
# library(MKmisc)
model=glm(Retention~.,
data=Retention.data.2,
family=binomial)
Pihat=predict(model,
type="response")
# HLgof.test(fit=Pihat,obs=Retention)Visualizing HLgof.test
hlgof=function(pihat,Y,ngr){
sortframe=sort(pihat,index=TRUE)
pihat=sortframe$x
Y=Y[sortframe$ix]
s=floor(length(pihat)/ngr) #groupsize
pipred=1:ngr
piobs=1:ngr
Chat=0
for(i in 1:ngr){
index=(((i-1)*s+1):(i*s))
if(i==ngr){index=(((i-1)*s+1):(length(pihat)))}
pipred[i]=mean(pihat[index])
nk=length(index)
ok=sum(Y[index])
piobs[i]=ok/nk
Chat=Chat+(ok-nk*pipred[i])^2/(nk*pipred[i]*(1-pipred[i]))}
pvalue=1-pchisq(Chat,ngr-2)
return(list(pipred=pipred,piobs=piobs,Chat=Chat,pvalue=pvalue))}
hlgof.results=hlgof(Pihat,Retention,10)Comparing Pihat and Piobs
plot(hlgof.results$pipred,hlgof.results$piobs,
xlim=c(0,1),
ylim=c(0,1))
lines((1:100)/100,(1:100)/100,col="red")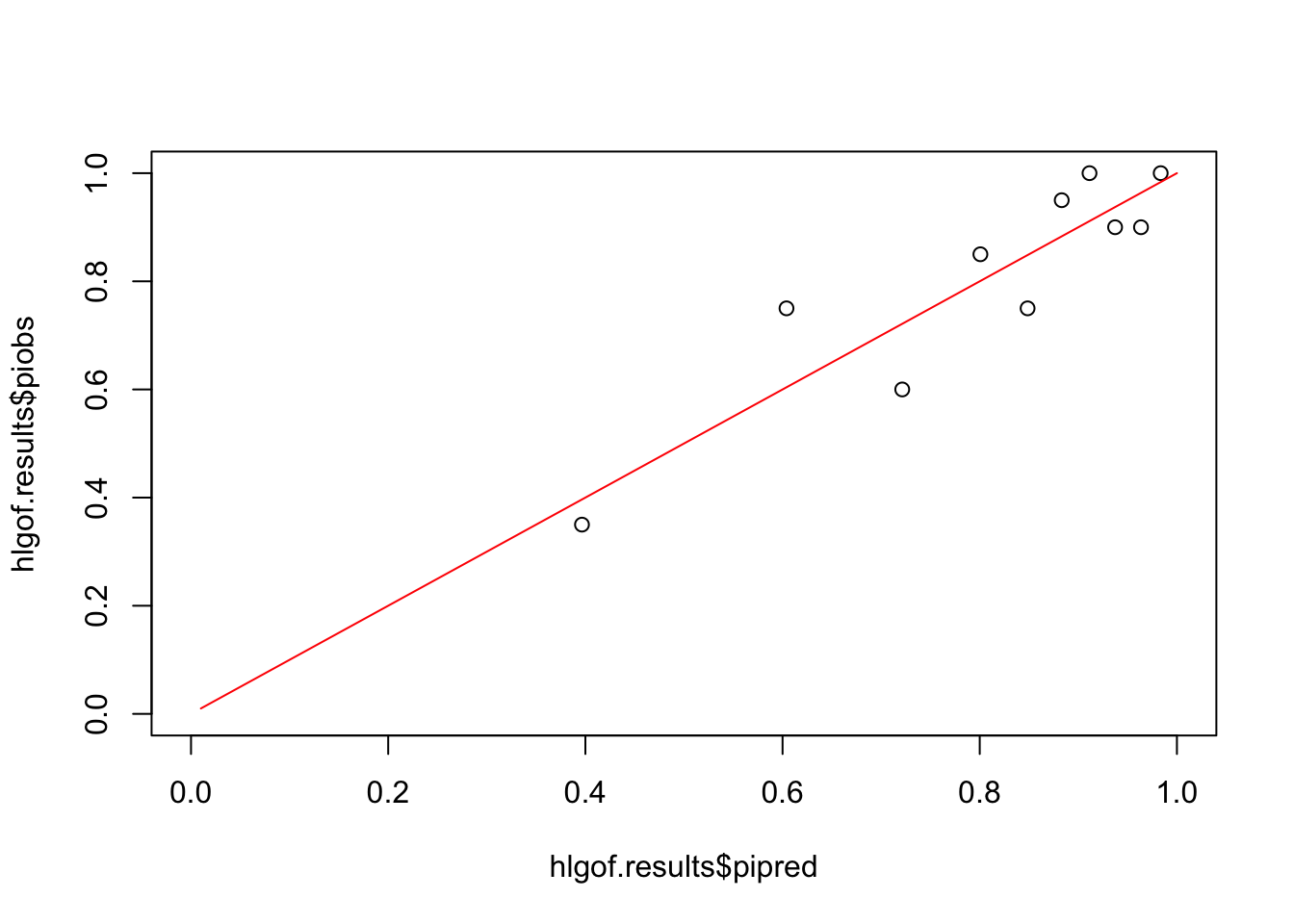
## piobs pipred
## [1,] 0.35 0.3965338
## [2,] 0.75 0.6039958
## [3,] 0.60 0.7213944
## [4,] 0.85 0.8006625
## [5,] 0.75 0.8485368
## [6,] 0.95 0.8831521
## [7,] 1.00 0.9113384
## [8,] 0.90 0.9372917
## [9,] 0.90 0.9635551
## [10,] 1.00 0.9835395## piobs pipred
## [1,] 7 7.930676
## [2,] 15 12.079916
## [3,] 12 14.427888
## [4,] 17 16.013249
## [5,] 15 16.970736
## [6,] 19 17.663041
## [7,] 20 18.226769
## [8,] 18 18.745833
## [9,] 18 19.271102
## [10,] 20 19.670789## [1] 11.1661